Triangular Numbers
Have you ever wondered? What is common in handshakes, mystic rose, third diagonal of pascals triangle, Sum of first n natural numbers : Triangular Numbers...
Mathematics is defined as the science of patterns! An interesting pattern can arise in so many different situations and places. One such example is of triangular numbers.
In daily life you might have seen triangular pattern of arranging vegetables in market or logs arranged in arrays wider at the base and tapering at the top.
Similarly bowling pins are arranged in triangular pattern- starting at one in first row and 4 in the last row.
Let's see how this particular pattern is generated in other situations!
Greetings_Handshakes_Mathematics!
Let us have a warm beginning with a handshake!
- If everyone in this group/class shook hands with everyone else, once only. How many handshakes would have taken place? Whenever this question is posed the most lucrative answer is half, sometimes it is said that just multiply the number with one less number and so on.
- Suppose there are 30 people in the room. In most of the sessions the answer that I have got is 15, or 30X 29= 870, sometimes 30!... in some occasions I get oh it's combinotorial problem, sometimes it becomes permutations and combinations- nCr and so many other possibilities of answers.
However, when the question arises why? and how? its quite challenging to describe.
Lets make it simple!
One of the most efficient strategy of problem solving in mathematics is breaking down the problem in smaller units/ parts.
Let's make it for 5 people. How many hand shakes in all of 5 people in a group.
I often asked 5 participants to get up one by one and check how many hand shakes could arise.
Let also arrange it one by one at the same time
(There is a cute element of surprise! Just ask the participants to guess about the total handshakes. For example call one person. how many handshakes would be there? None!since we have not defined self handshake, now if two are there there will be one, if three, there would be how many? Most of the time the answer I get from the participants is 2- but when they actually perform the activity they realise it is 3. This sparks enthusiasm amongst the participants and you can make it much more interesting by adding your own style, while explaining further numbers of handshakes. It is observed that the participants starts identifying the pattern and how it is being developed.)
This is the time to ask for some higher order questions:
- How many handshakes will be there for everyone in this workshop?
- Everyone in your school?
- How can you be sure that your method works?
So along with relationships can we come up with some generalisations
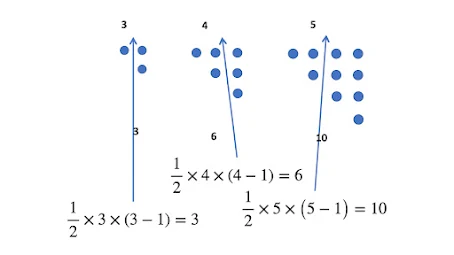
Number of handshakes for n people = ½ X (n) X (n-1)
Is there any other way this rule can be derived?
Just by arranging the triangular dots in the form of a rectangle we can see that the half of the area of the rectangles would be the required triangular numbers!
So we can conclude that,
Half of the area of rectangle with sides n & (n-1) = ½ X (n) X (n-1)
Definition of Triangular number
A triangular number or triangle number counts objects arranged in an equilateral triangle
The nth triangular number is the number of dots in the triangular arrangement with n dots on each side, and is equal to the sum of the n natural numbers from 1 to n.
0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435, 465, 496, 528, 561, 595, 630, 666…
Story: The Wunderkid Carl
This is a very interesting story about The Wonderkid Carl.
One day his primary school teacher asked the entire class to add together all the numbers from 1 to 100. He thought this will occupy the students for a while. After a few seconds Carl came up with the answer- 5050. The teacher was completely shocked how could this young kid come up with this answer so quickly. Carl pointed out that the problem was actually very simple
He just wrote few numbers in the beginning and in the end and saw a relationship between them in the following form.
This was amazing that a child in primary school has discovered this simple method for summing sequences of number.
This wonderkid was Carl Friedrich Gauss (1777-1855), one of the greatest mathematicians of all time. During his lifetime he made significant contributions to almost every area of mathematics, as well as physics, astronomy and statistics.
Gauss's method forms a general formula for the sum of the first n integers, namely that 1+2+3+…+n= n(n+1)
Mystic Rose Pattern
A beautiful and creative activity that is related to triangular number can be easily done with easily available and simple paper- pencil and a ruler.
Steps:
1. Draw a circle.
2. Take six points at equal distance from each other on the circumference
3. Start with any one point and join the other points with straight lines using colour pencils/ pens.
4. Now take the neighbouring point and start joining the remaining points
5. Use your own colour combinations
How can you relate this with triangular numbers?
Pascals triangle and Triangular numbers
A worksheet can be given to the students to come up with interesting patterns that they can create with inserting numbers in the slots.
Can you find a relationship here with triangular numbers?
Though Greeks were fascinated with triangular numbers, even today there are lot of applications of Triangular numbers.
They are great starting point for the children to get familiarised with numbers, sequences and the different patterns that are formed. It is also interesting to note how numbers can be expressed as geometrical shapes. Understanding Triangular numbers is a good example of interrelation between arithmetic, algebra and geometry!
References:
1. https://nrich.maths.org/
3. (https://en.wikipedia.org/wiki/Triangular_number









Comments
Post a Comment